Graf renklendirme de kullanılan algoritmalardan birisi Welch ve Powel’in önerdiği yöntemdir. Bu yöntem genel olarak düğümlerin derecelerine dayanmaktadır. Renklendirmede kullanılan toplam renk sayısı kromatik (chromatik) sayı olarak adlandırılır. Algoritmanın davranışı adım adım aşağıdaki gibidir.
- Düğümler derecelerine göre büyükten küçüğe doğru sıralanır.
- İlk renk birinci sıradaki düğüme ve bu düğümün komşusu olmayan düğümlere atanır.
- Bir sonraki renge geçilir ve bu renk sıradaki derecesi en yüksek olan düğüme ve bu düğümün komşusu olmayan düğümlere atanır.
- Süreç bu şekilde renklendirilmemiş düğüm kalmayana kadar devam ettirilir.
Yukarıdaki algoritmayı aşağıdaki örnek graf üzerinde açıklayacak olursak;
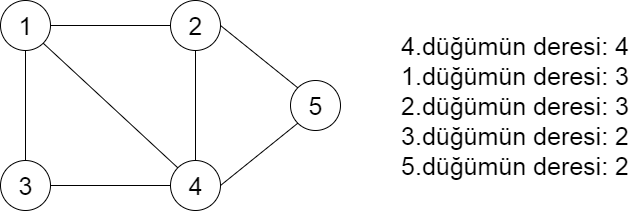
1.İlk renk birinci sıradaki düğüme atanır (en yüksek derecesi olan) ve daha sonra aynı renk birbirlerine bitişik olmayacak biçimde diğer düğümlere verilir.
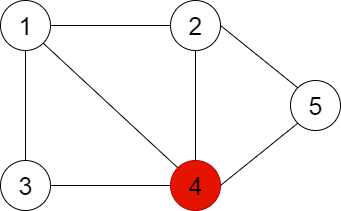
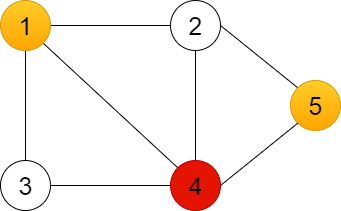
2.Bir sonraki renge geçilir, bu renk sıradaki derecesi en yüksek olan düğüme atanır; ve sonra bu renk, daha önce renklendirilmemiş düğümlere birbirlerine bitişi olmayacak şekilde atanır.
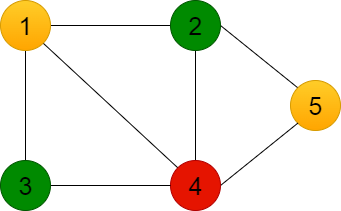
4.Tüm düğümlere renk verilinceye kadar işlem tekrar edilir.
Uygulama Alanları;
- Harita renklendirme,
- İşlemcilerin işlem sırasını belirleme,
- Ders ve sınav programı ayarlama
- Hava alanlarında iniş ve kalkış sırasını belirleme vs.
Uygulamada, graf renklendirmenin kullanılacağı alanların başında, ilk akla gelen, harita üzerindeki bölgelerin renklendirilmesi olabilir. Graf renklendirme bilgisayar biliminde ve günlük yaşamdaki birçok problemin çözümüne ciddi bir yaklaşımdır. Şimde de günlük hayatımız da kullandığımız graf renklendirme işlemini, çakışmadan sınav oturumlarının belirlenmesi örneğinde inceleyeceğiz.
Problem
Bir üniversitede final sınavları öyle yerleştirilmek istenmektedir ki öğrencilerin farklı derslerine ait sınavları çakışmasın. Üniversitede 4 tane öğrenci ve 6 tane ders vardır ve herhangi bir öğrenci tabi ki aynı anda birden çok ders almaktadır. Bir de elimizde hangi öğrencinin hangi dersleri aldığı liste vardır.
4 tane öğrenci 6 tane ders varsa ilgili kümelerimiz:
D={d0, d1, d2, d3, d4, d5}
Ö={Öğrenci-1, Öğrenci-2, Öğrenci-3, Öğrenci-4}
Her bir öğrencinin aldığı dersler de aşağıdaki gibi olsun:
Öğrenci-1: d0, d1, d4 Öğrenci-2: d0, d2, d4
Öğrenci-3: d2, d3, d5 Öğrenci-4: d3, d4, d5
Soru: Herhangi bir öğrencinin sınavı çakışmayacak şekilde yerleştirme yapılmasına yönelik olarak sınavlar için kaç farklı oturum gerektiği ve aynı anda hangi derslere ait sınavların yapılabileceğini belirleyiniz.
Çözüm:
Bu problem graf renklendirme ile çözülebilir. Dersler graf üzerindeki düğümler olarak kabul edilip öğrencilerin aldığı dersler de düğümler arasındaki hatları belirler. Bu grafın renklendirilmesi sonucu hangi dersin aynı anda yapılabileceği sonucu çıkar; aynı renge ait dersler aynı anda yapılabilir denilir. Kromatik sayı sınavların yapılması için gerekli toplam oturum sayısını verir.
İlk yapılması gereken bu verilerden ilgili grafın ortaya çıkarılmasıdır; derslerin kendileri grafın düğümlerini,
alınan dersler de düğümler arasındaki bağlantıyı belirler.

Graf elde edildikten sonra Welch ve Powel algoritmasına göre düğümler derecelerine göre sıralanır. En yüksek dereceli düğüme ilk renk atanır.
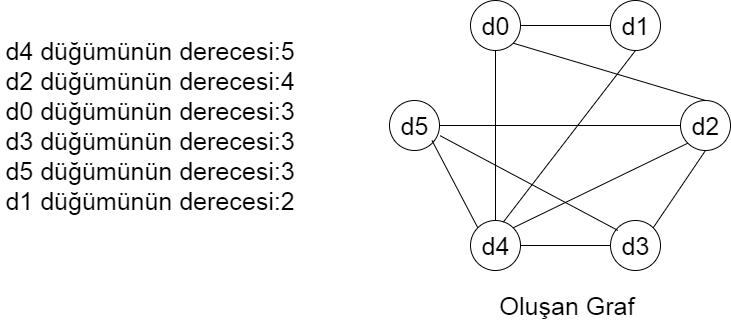
Welch ve Powel algoritmasına göre renklendirilirse aynı renge sahip olan dersler arasında ilişki olmadığı ve sınavların aynı anda yapılabileceği ortaya çıkar.
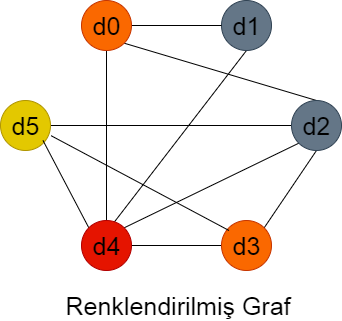
Dolayısıyla Sonuç
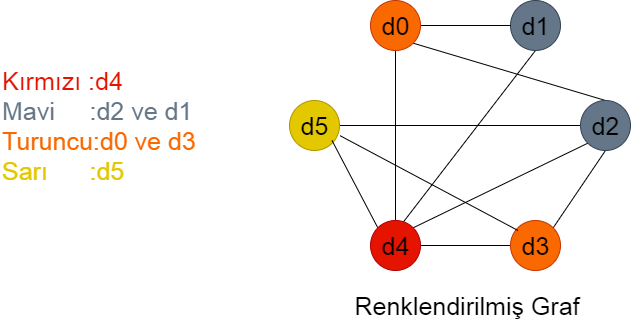
Kromatik sayı 4 çıkmıştır; toplam dört oturum yapılmalıdır. Buna göre d4 dersinin ve d5 dersinin sınavı tek başına ayrı oturumlarda yapılmalıdır; ancak d2 ile d1 veya d0 ile d3 derslerinin sınavları aynı anda yapılabilir.
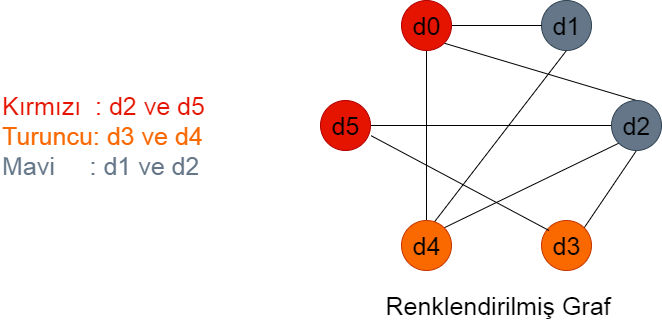
Soru: Öğrenci-4 d4 dersini almaktan vazgeçip bırakırsa sınav yerleştirimi nasıl olur?
Bu durumda Öğrenci-4’ün alacağı dersler d3 ve d5 olacaktır ve daha önce d4’den dolayı oluşan d3-d4 ve d4-d5 hatları, eğer bu kenarlar başka bir öğrenci tarafından da oluşturulmuyorsa graftan çıkarılacaktır. Bu durumda grafın yeni durumu ve renklendirme aşağıdaki gibi olur.
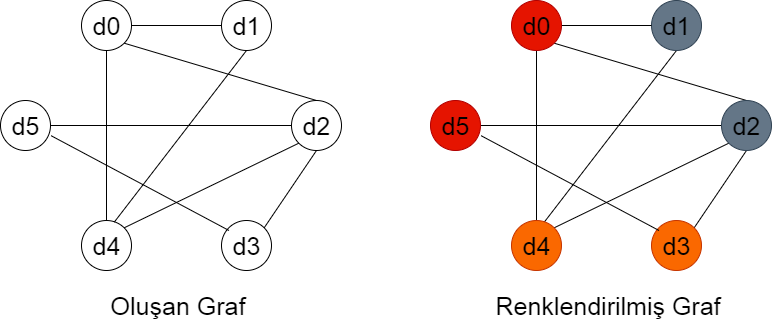
Görüldüğü gibi kromatik sayı 3 çıkmıştır; bu durumda tüm oturum yeterlidir ve derslere ait sınavları aşağıdaki gibi yapılabilir:
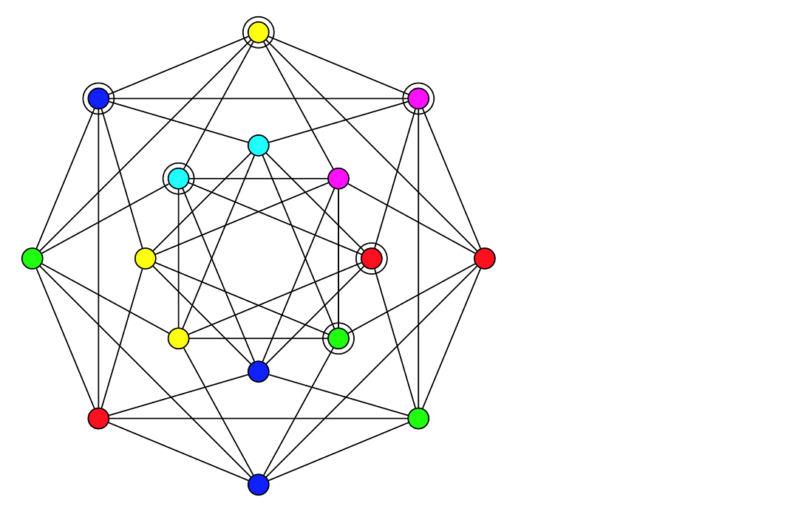
Not:Düzlemsel bir G=(D, K) grafı en fazla 4 renk kullanılarak renklendirilebilir; yani, kromatik sayı 4’tür.
Kaynakça: Geeksforgeeks, Princeton,
Gould, R. (Ed.). Graph Theory. Menlo Park, CA: Benjamin-Cummings, 1988.
Lec 6 | MIT 6.042J Mathematics for Computer Science, Fall 2010 | Video Lecture






Yorum Yap