Enine Arama (Breadth-first Search)

Bilgisayar biliminde, sığ öncelikli arama ya da enine arama, bir çizgenin düğümlerini, başlangıç noktasına daha yakın olanlara öncelik vererek arayan bir algoritmadır. Enine arama algoritması ziyaret ettiği düğümlerin bütün komşularını bir kuyruğa ekler ve ziyaret edeceği düğümleri kuyruktaki sıraya göre seçer. Eğer arama yapılan çizge bir ağaç ise kuyruk kullanmaya gerek olmaz.

Bir çizge aramasındaki en basit algoritmalardan biridir ve pek çok önemli çizge algoritmasının ilk örneğidir. Prim’in minumum kapsayan ağaç algoritması ve Dijkstra’nın tek kaynaklı en kısa yollar algoritması ile benzer fikirleri kullanır. Algoritma yönlü ve yönsüz çizgelerin her ikisi içinde çalışır.

Sığ öncelikli arama 1945’te Michael Burke ve Konrad Zuse tarafından çizgelerde bağlı bileşenleri tespit etmek için geliştirilmiştir. Ancak, bu algoritmanın sunulduğu doktora tezi kabul edilmemiştir ve 1972 yılında yayınlanmıştır. 1959’da E. F. Moore tarafından, bir labirentteki en kısa yolu bulmak için, 1961 yılında ondan bağımsız bir şekilde C. Y. Lee tarafından devrelerde bağlantıların belirlenmesi amacıyla tekrar icat edilmiştir.

Nasıl Çalışır?

İlerleme yolunu bulmak için algoritma her tepeyi beyaz, gri veya siyah renkle boyar. Tüm tepeler beyaz ile başlar, sonradan gri ve en son siyah olur. Arama sırasında bir tepe ile ilk defa karşılaşıldığında o tepe bulunan (discovered) olur ve o andan itibaren tepe artık beyaz renkli değildir. Gri ve siyah tepeler bulunan tepelerdir, fakat enine ilerlemek için bunlar arasından hangisinin seçileceğine karar verilir. Eğer (u,v) ∈ E ve u tepesi siyah ise, v tepesi de siyah veya gridir, böylece siyah tepelere bitişik olan tüm tepeler gezilir. Gri tepeler bazı beyaz tepelerle bitişik olabilir; bulunan ve bulunmayan tepeler arasındaki sınırı gösterirler.

Enine arama başlangıçta sadece s kaynak tepesi olan kökü içererek enine ağacı oluşturur. Daha önce bulunan u tepesinin bitişiklik listesi gezinirken beyaz v tepesi bulunduğunda v tepesi ve (u,v) ayrıtı ağaca eklenir. u tepesine v‘nin öncülü(predecessor) ya da ebeveyni (parent) denir. Bir tepe en fazla bir kez bulunduğundan, en fazla bir ebeveyni olur. Enine ağaçta s köküne bağlı olarak ata (ancestor) ve torun(descendant) ilişkisi şu şekilde tanımlanır: eğer ağaçta s kökünden v tepesine olan basit yolda u tepesi varsa, bu durumda u, v nin atası v de u nun torunu olarak isimlendirilir.

Aşağıda yer alan BFS enine arama işlemi, girdi çizgeyi G = (V, E) nin bitişiklik listesi kullanılarak gösterildiğini varsayar. Çizgede her tepeye birkaç ek özellik ilave eder. Her u ∈ V tepesinin rengini u.color özelliği ile ve u nun öncülünü (predecessor) ise u.π özelliği içinde saklarız. Eğer u, öncül tepeye sahip değilse (örneğin eğer u=s veya u henüz bulunmayan bir tepeyse) bu durumda u.π = NIL olur. u.d özelliği ile algoritma tarafından hesaplanan s kaynağından u tepesine olan uzaklık tutulur. Gri teplerin kümesini kontrol etmek için algoritma ayrıca ilk-giriş, ilk-çıkış kuyruğu Q yu kullanır.

Sözde Kod

BFS (G.s)
  for her u∈ G.V - {s} tepesi
      u.color = ∈WHİTE
      u.d = ∞
      u.π= NIL
  s.color = GRAY
  s.d = NIL
  Q = Ø
  ENQUEUE(Q,s)
  while Q ≠ Ø
      u= DEQUEUE(Q)
  for her v ∈ G.Adj[u]
      if v.color == WHİTE
         v.color =GRAY
         v.d = u.d + 1
         v.π = u
         ENQUEUE(Q,v)
      u.color = BLACK

Aşağıda örnek üzerinde BFS’nin ilerleme durumunu göstermektedir.

BFS işlemi aşağıdaki gibi çalışmaktadır. s kaynak tepesi hariç, satır 1-4 her tepeyi beyaza boyar, her u tepesi için u.d yi sonsuz olarak belirler ve her tepenin ebeveynini(parent) NIL olarak belirler. Satır 5, işlemler başladığında bulunan olarak düşündüğümüz s tepesini griye boyar. Satır 6, s.d yi 0 olarak başlatır ve satır7 kaynağın öncülünü (predecessor) NIL olarak belirler. Satır 8-9 sadece s tepesini içeren Q kuyruğunu başlatır.

Satır 10-18 deki while döngüsü, bitişiklik listesi tam olarak elden geçirilmemiş bulunan tepeler yani gri tepeler kaldıkça tekrarlanır. Bu while döngüsü aşağıdaki değişmezi korur.

Satır 10 daki testte, Q kuyruğu gri tepeler kümesinden oluşur.

Örnek

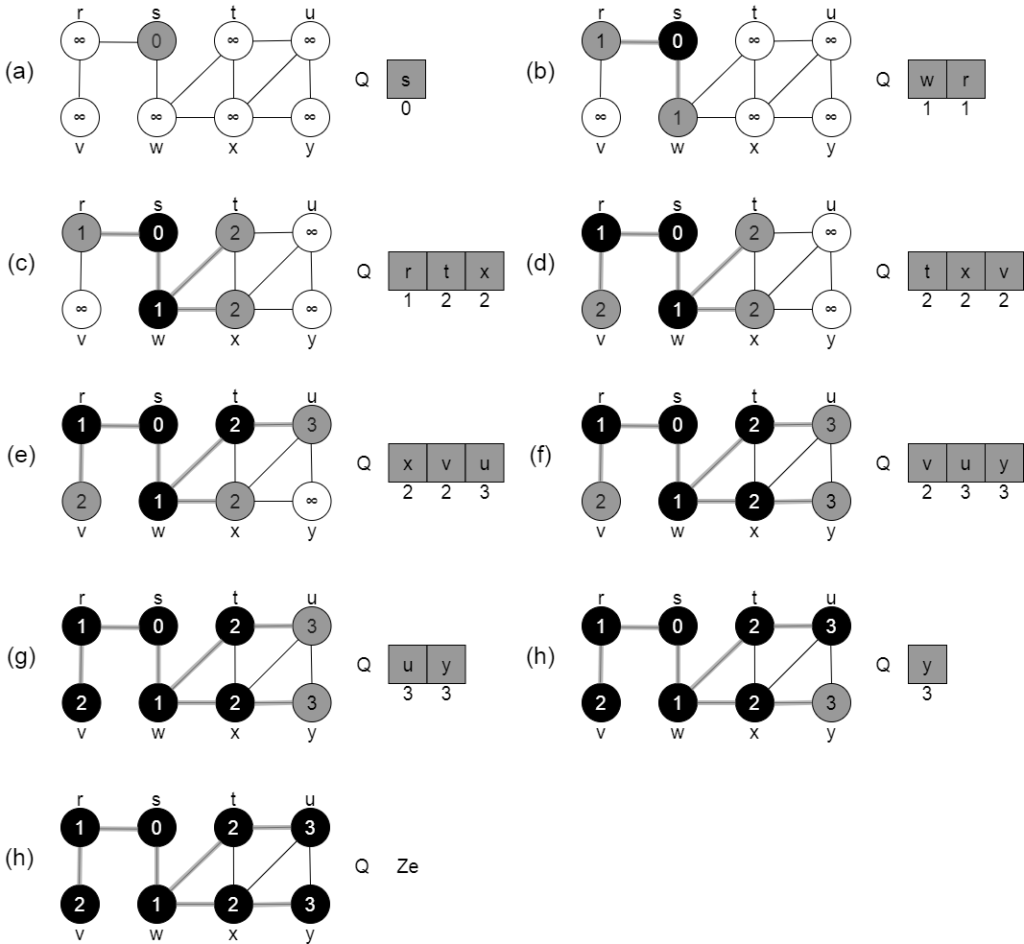
İlk iterasyona (a) göre Q kuyruğundaki tek gri tepe ve tek tepe, s kaynak tepesidir. Satır 11, Q kuyruğunun en başındaki u gri tepesini ele alarak onu Q dan atar. Satır 12-17 deki for döngüsü u nun bitişiklik listesindeki her ve tepesini inceler. Eğer v beyaz ise, henüz keşfedilmemiştir ve satır 14-17 nin çalıştırılması ile işlem onu keşfeder. İşlem v tepesini griye boyar, uzaklığını v.d iken u.d+1 ye olarak belirler, u nun ebeveyni olarak v.π yi kaybeder v onu Q kuyruğunun en sonuna yerleştirir. u nun bitişiklik listesindeki tüm tepeler işlem tarafından bir kez daha incelenir incelenmez satır 18 onu siyaha boyar. Döngü değişmezi korunur çünkü bi tepe griye boyandığında (satır 14 de) o aynı zamanda sıraya alınır (satır 17 de) ve bir tepe kuruktan çıkarıldığında (satır 11 de) o aynı zamanda siyaha boyanır(satır 18 de).

Enine aramanın sonuçları verilen bir tepenin komşularının satır 12 de ziyaret edilme derecesine bağlı olabilmektedir; enine ağaç farklı olabilir, fakat algoritma ile hesaplanmış olan d uzaklıkları farklı değildir.

Kaynakça: Wikipedia, Geeksforgeeks, Hackerearth, Tutorialspoint

Bilgisayar Kavramı

U.NURİYEV, E.NASİBOĞLU, T. ÖNER. (2017). Algoritmalara Giriş Ankara: Palme Yayıncılık (589-602)