Bellman-Ford algoritmasının amacı, bir şekil (graph) üzerindeki, bir kaynaktan (source) bir hedefe(target ) giden en kısa yolu bulmaktır. Bir s ∈ V kaynağından tüm v ∈ V’lere bütün kısa yol uzunluklarını bulur. Yada bir negatif ağırlık çevrimi olduğunu saptar. Algoritma ağırlıklı şekiller (weighted graph) üzerinde çalışır ve bir anlamda Dijkstra algoritmasının iyileştirilmişi olarak düşünülebilir.
Algoritma aslında Dijkstra algoritmasından daha kötü bir performansa sahiptir ancak graftaki ağırlıkların eksi(-) olması durumunda Dijkstra’nın tersine başarılı çalışır.
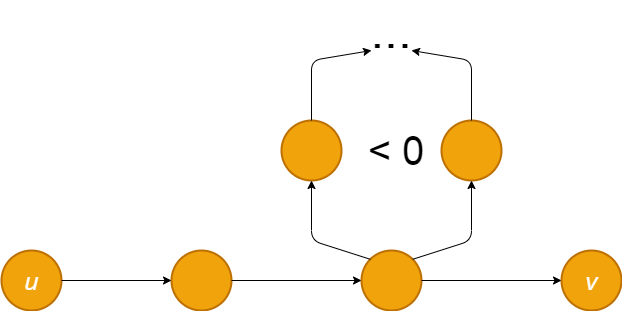
- Her düğüm için bir uzaklık tahmini oluşturulur.
- Başlangıç olarak maliyet(s)=0 diğer düğümler için maliyet(u)= ∞ olarak atanır.
- En az maliyetli yol hesaplanana kadar tüm kenarlar üzerinden güncelleme yapılır.
BELLMAN-FORD(G,w,s)
d[s] ← 0
for each v ∈V –{s}
do d[v] ← ∞
for i ← 1 to |V| - 1
do for each edge (u,v) ∈E
do if d[v] > d[u] + w(u, v)
then d[v] ← d[u] + w(u, v)
for each edge (u,v) ∈ E
do if d[v] > d[u] + w(u,v)
then bir negatif ağırlık döngüsünün var olduğunu bildirin.
return d[v] // = δ(s, u), negatif ağırlıklı döngü yoksaBu algoritmanın çalışmasını örnek bir şekil( graph ) üzerinden göstermeye çalışacağım. Bu gösterimin ardından Bellman-Ford Algoritmasının başarısını ve eksik taraflarını tartışabiliriz.
Aşama 0
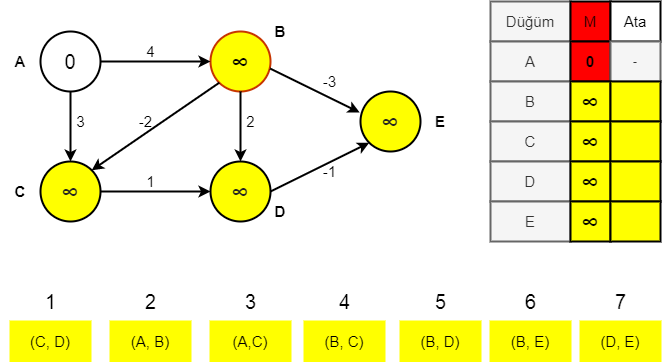
Algoritmanın çalışmasını yukarıdaki gibi eksi değerlere sahip bir şekil üzerinden anlamaya çalışalım.
Öncelikle düğümlere değer ataması yapılıyor. Başlangıç düğümüne 0, doğrudan erişilen düğümlere erişim değerleri ve erişilemeyen düğümlere ∞ sonsuz değeri atanıyor. Hedef düğüm olarak da E düğümünü tanımlayalım.
Aşama 1
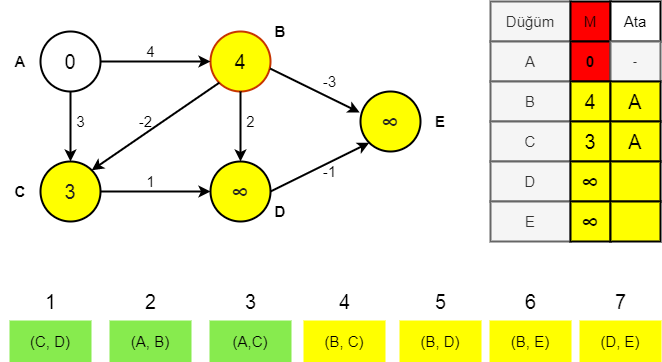
Bellman ford algoritması işte bu kenarları teker teker dolaşması itibariyle dijkstradan ayrılır. Sırayla yukarıdaki kenarları (Edges) dolaşır ve graftaki değerleri günceller.
İlk yineleme
B=AB 4, min(A,B)= 0-> 0+4 = 4
Aşama 2
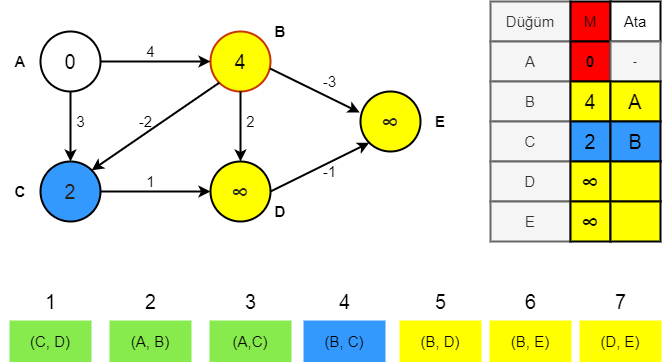
C=AC 3, min(A,C)=0->0+3 =3
C= BC -2, min(B,C)= 4-> 4-2 = 2
Aşama 3
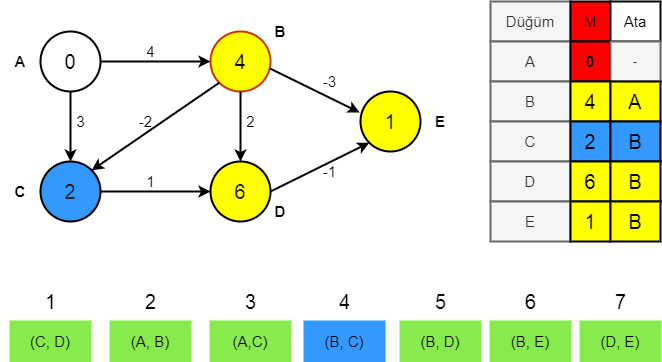
D=BD 2, min(B,D)=4->4+2 =6
Aşama 4
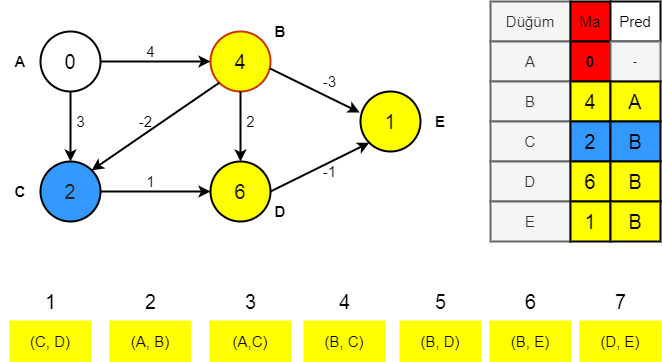
E= BE -3, min(B,C)= 4-> 4-3 = 1
1.Tur sonu
Aşama 5
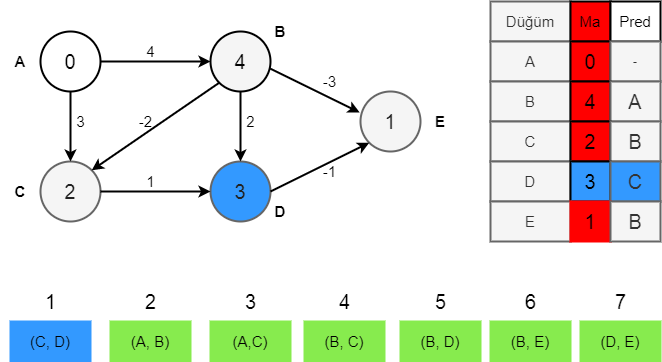
D=CD 1, min(C,D)= 2-> 2+1 =3
2.Tur Yineleme
Aşama 6
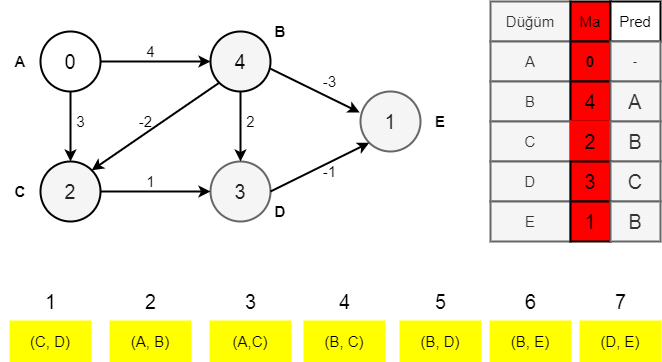
Üçüncü & Dördüncü Yineleme
Aşama 7
Sonuç:
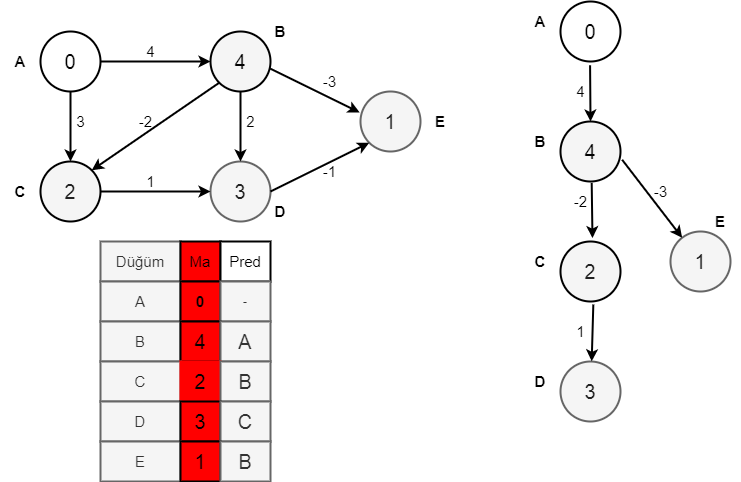
Negatif ağırlıklar için geliştirişmiş genel ağırlıklar için Bellman-Ford algoritmasından bahsedildi ve çalışma zamanı O(VE)‘ye mal olmaktaydı.
Kaynakça: Wikipedia, Techiedelight, Geeksforgeeks
MIT Introduction to Algorithms 6.046J/18.401J/SMA5503 Lecture 18 Prof.Erik Demaine







Yorum Yap