Türkçesi “ Derinlik öncelikli arama ” şeklinde geçen DFS bizim belirlediğimiz bir kök node’dan başlıyor ve herhangi bir çocuğunu seçiyor. Daha sonra bu çocuktan daha önce gezmediğimiz herhangi bir node’a gidiliyor. Bu seçimlerdeki iki kuralımız var birincisi seçeceğimiz node’a direkt yol olmalı diğeri ise o node daha önce gezilmemiş olmalı. Bu kuralları uygulayarak rekürsif bir şekilde geziliyor.
Ancak öyle bir node’a geliyoruz ki gidilecek yer kalmıyor. Çünkü direkt bağlantımızın olduğu bütün node’lar daha önceden gezilmiş. Böyle bir durumda ise bu node’dan önce en son gezdiğimiz node’a geri dönüyoruz ve başka tercihler var mı diye bakıyoruz. Algoritma rekürsif olarak çalıştığı için her takıldığımız noktada bir üste çıkmamıza olanak sağlıyor. Algoritmamız başladığımız yere geldiğimizde ve hali hazırda bütün çocuklarımızı gezdiğimizde bitiyor.
Sözde Kod
DFS(G)
for each u ∈ V do
color[u] <- white
pred[u] <- NIL
time <- 0
for each u ∈ V do
if color[u] = white
then
DFS-VISIT(G, u)
DFS-VISIT(G, u)
color[u]<- gray
d[u]<- time <- time + 1
for each v∈ Adj[u] do
if color[v] = white then
pred[v] <- u
DFS-VISIT(G, v)
color[u] <- black
f[u]<- time <- time + 1
Derin Öncelikli Arama İşlem Adımları:
- Önce bir başlangıç node’u seçilir ve ziyaret edilir.
- Seçilen node’un bir komşusu seçilir ve ziyaret edilir.
- 2.adım ziyaret edecek komşu kalmayıncaya kadar tekrar edilir.
- Komşu kalmadığında tekrar geri dönülür ve önceki ziyaret edilmiş node’lar için adım 2 ve 3 tekrar edilir.
Aşağıdaki somut örnek üzerinde söylediklerimizi inceleyelim.
Derin Öncelikli Arama Örneği
Aşama 1:
Her bir node’lar üzerinde gideceği komşuları belirlenir.
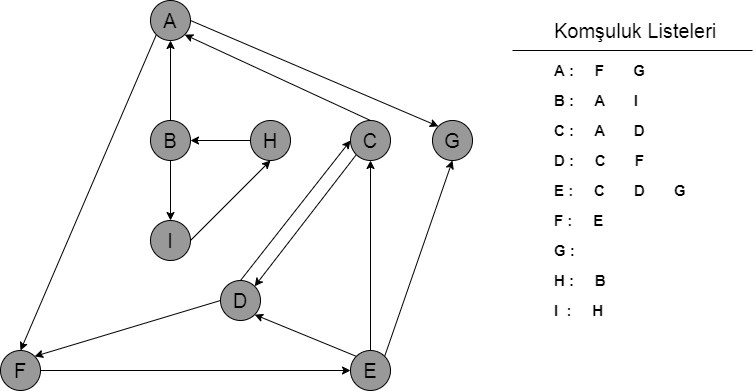
Aşama 2:
Öncelikle bir root (başlangıç node) seçmemiz gerekir. Root olarak A node’nu seçiyoruz. A’nın komşuları F ve G node’ları var.
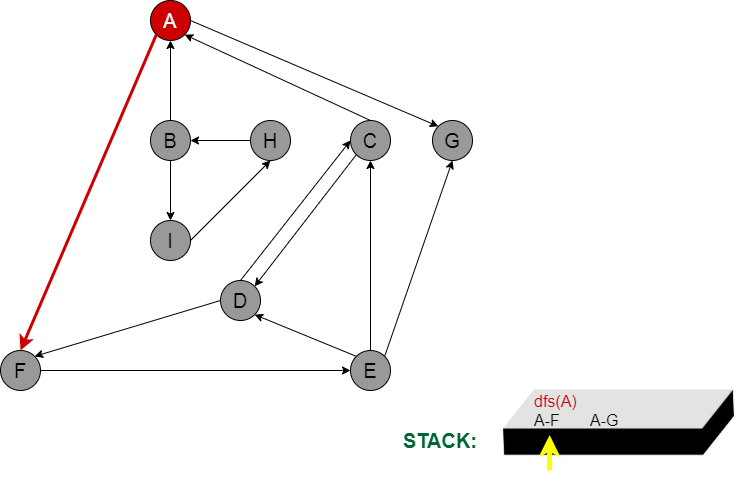
Stack’de A eklenmiş olur. A’nın gidebileceği F ve G node’ları vardır. Herhangi bir çocuğundan başlamamız lazım.
Aşama 3:
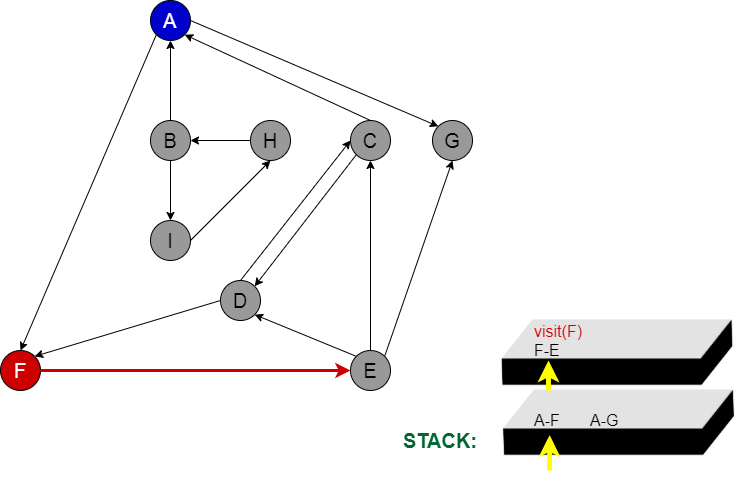
F seçelim. F’den direkt yol olan E node vardır. Böylelikle stacke F node da eklenmiş olur. F node’nun gidebileceği tek bir yer var. E node’na gitmiş oluyoruz.
Aşama 4:
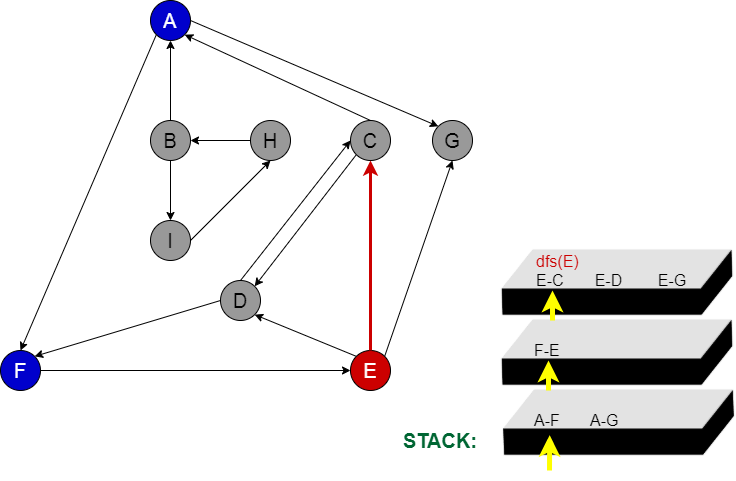
Stacke E node da eklenmiş olur. E’nin gidebileceği komşuları C, D ve G nodelarıdır. Örnekte C node’nu tercih ediyoruz.
Aşama 5:
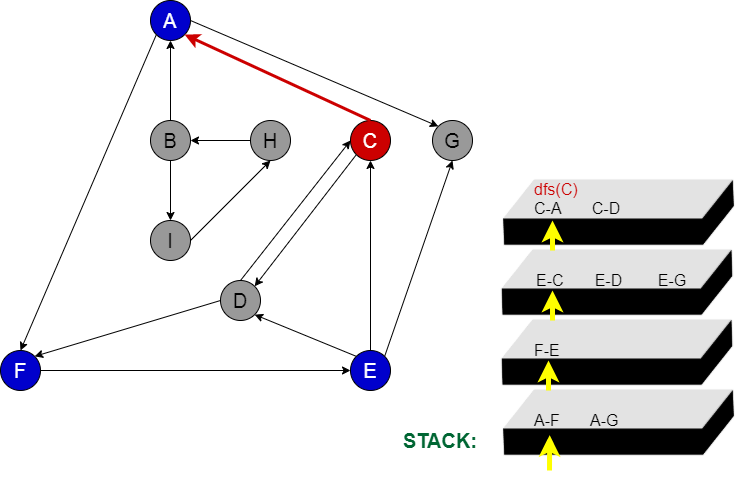
Stacke C node da eklenmiş olur. C node’dan A ve D nodelarına gidebiliriz. A node’ya gidiyoruz. A node’na daha önce uğradığımızı fark ederiz.
Aşama 6:
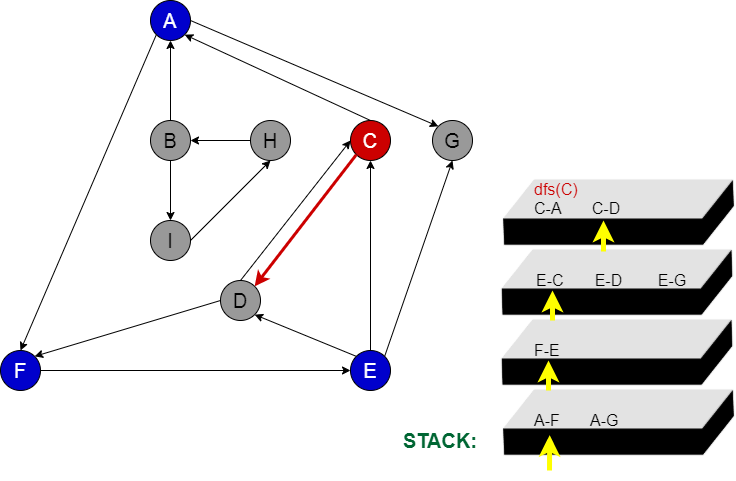
C node’dan A ya daha önce uğramış olduğumuz için C node’ndan D node’na gideriz.
Aşama 7:
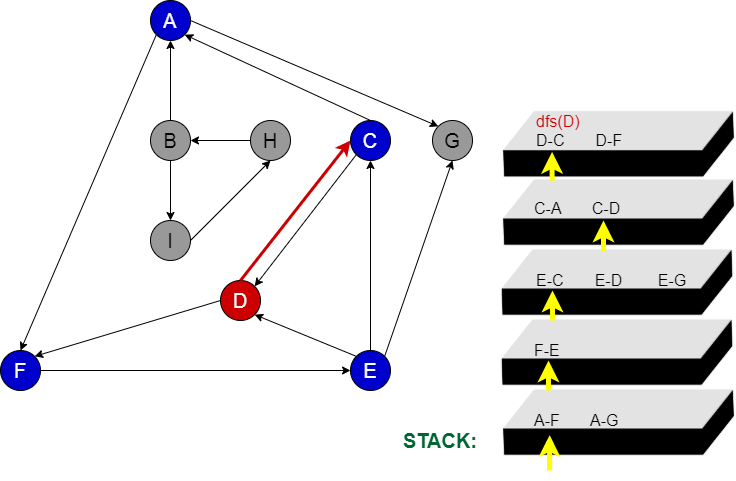
Daha önce D node’na uğramadığımız için D node’nu stacke ekleriz. D node’ndan gidebileceği komşular C ve F nodelarıdır. İlk tercihimiz. C node olur. Daha önce buraya uğradığımızı fark ederiz.
Aşama 8:
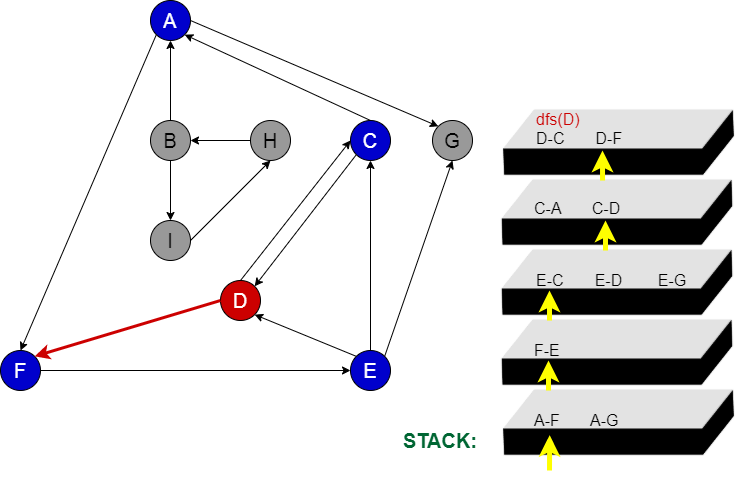
D node’ndan gidebileceği bir diğer node F node, orayada daha önce uğradığımızı biliyoruz.
Aşama 9:
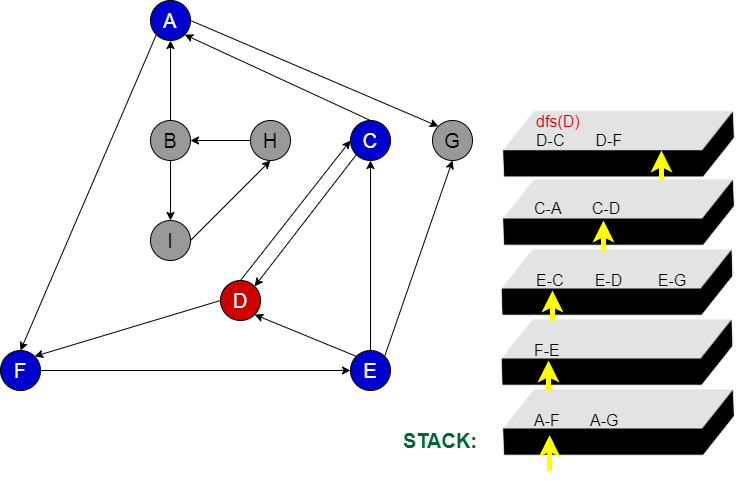
D node’nun gidebileceği başka hiçbir yer kalmadı.
Aşama 10:
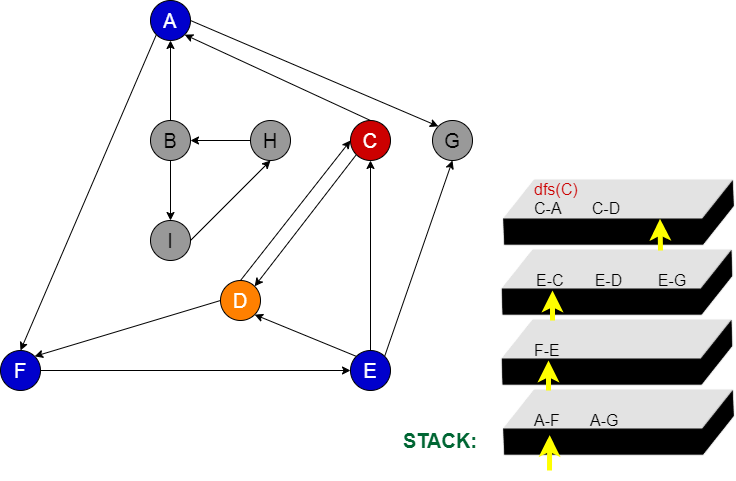
D node’nun gidebilecek yeri kalmadığı için stackten onu siliyoruz. Stackten sildiğimiz node peşine hangi node var ise oradan devam edilir.(C node)
C node’nun komşuları A ve D nodeları idi. A ve D nodelarını daha önce gitmiştik. Başka gidebileceğimiz yer kalmadığı için C node’nu stackten çıkarıyoruz.
Aşama 11:
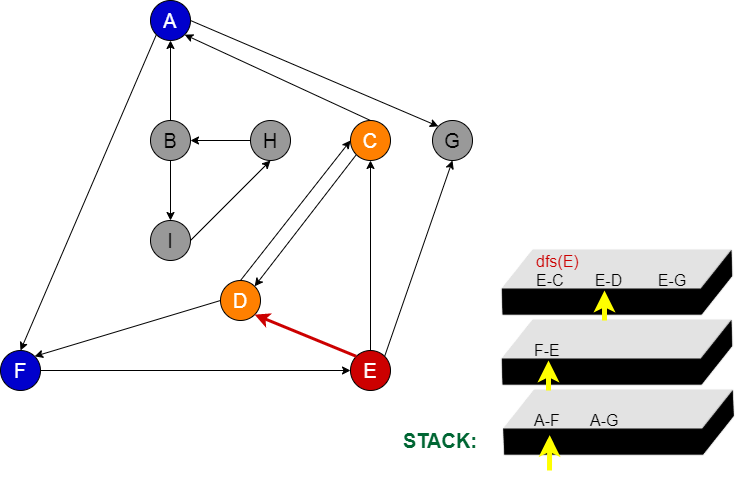
Stackten sildiğimiz node peşine hangi node var ise oradan devam edilir.(E node) E node ile daha önce C node’na gitmiştik. E node’ndan gidebileceğimiz komşular D ve G kaldı. D node’na gittiğimizde, D node’na daha önceden uğradığımızı görüyoruz.
Aşama 12:
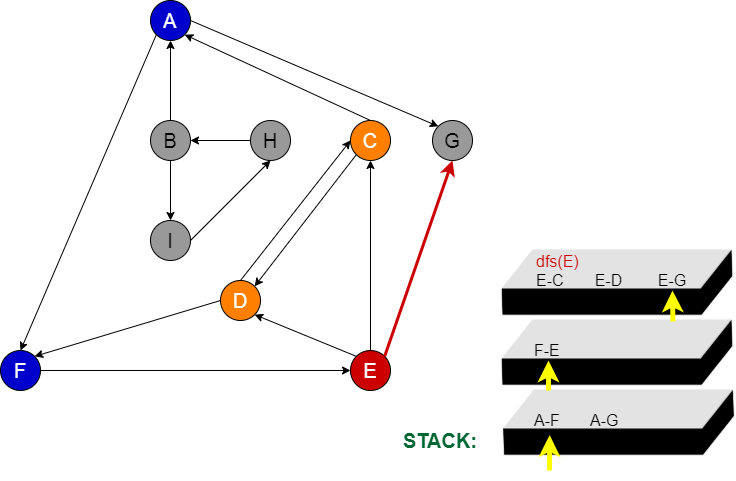
E node’ndan gidebileceğimiz G node kaldı. G node’na daha önceden uğramamışız.
Aşama 13:
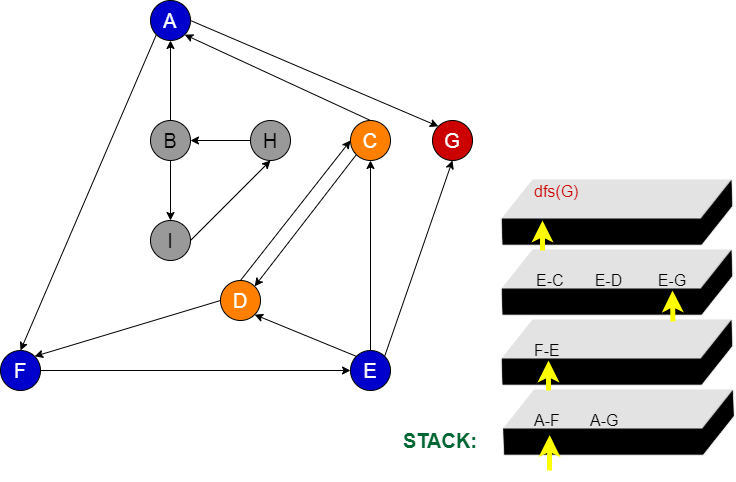
G node’nu stacke eklenir. G node’ndan gidebileceğimiz komşu node’lar yoktur. G node’nu da stackten silebiliriz.
Aşama 14:
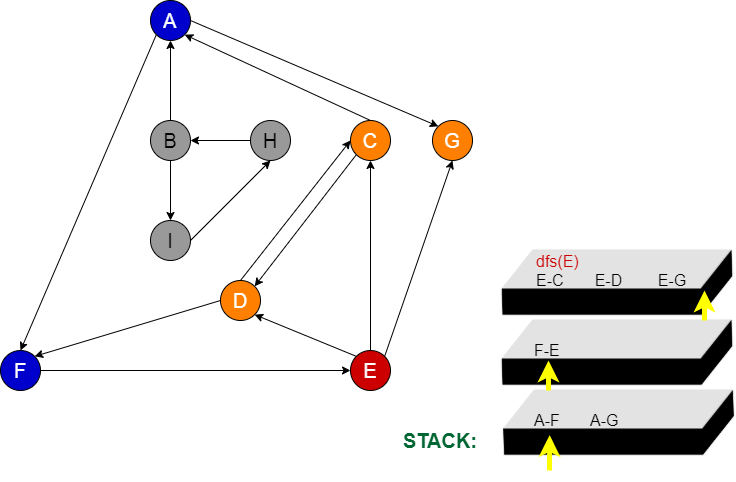
Stackten sildiğimiz node peşine hangi node var ise oradan devam edilir.(E node) E node’nun komşuları C, D ve G hepsine uğramış olduk. E node’nun gidebileceği başka bir yer kalmadığı için E node da stackten sileriz.
Aşama 15:
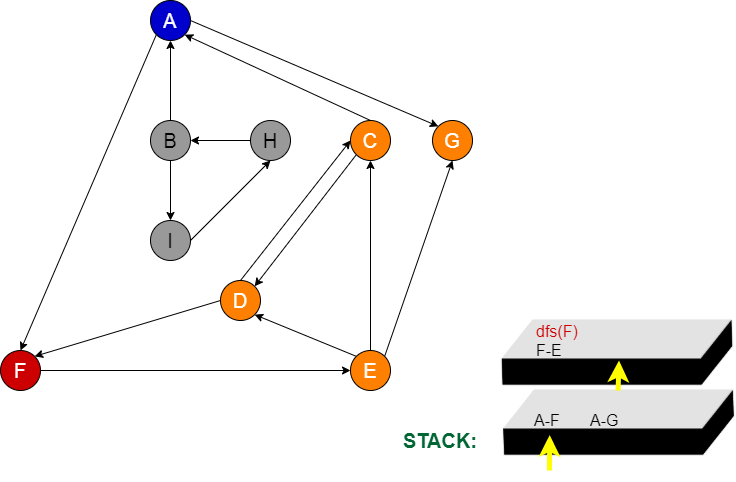
Stackten sildiğimiz node peşine hangi node var ise oradan devam edilir.(F node) F node’nun gidebileceği E node var. E node’na da daha önce uğradığı için gidecek başka bir yer kalmadı. F node stackten silinir.
Aşama 16:
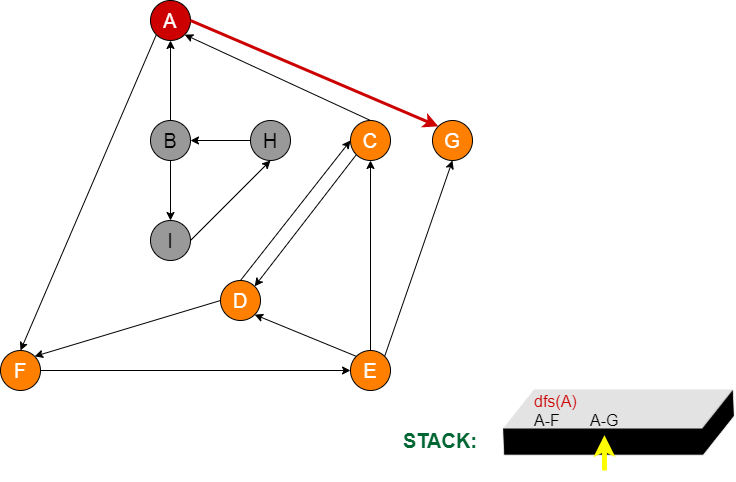
Stack’te sadece A node kalır. A’nın komşuları F ve G node’larıdır. F’ye daha önce uğradığı için G node’na giden yolu kullanır.
Aşama 17:
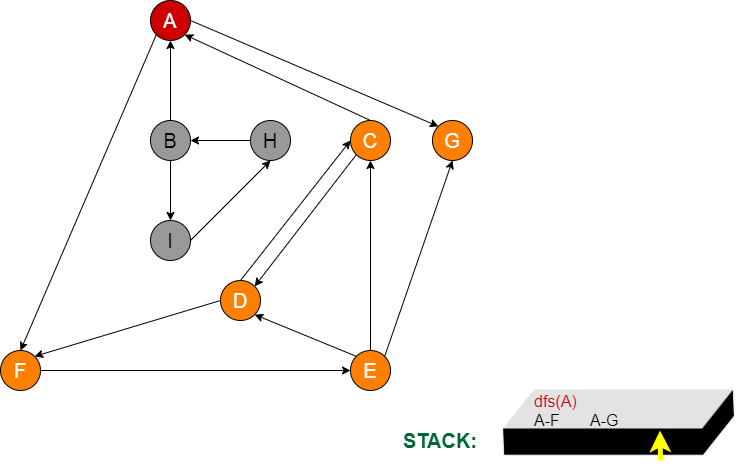
G’ye daha önce uğramış olduğumuz için A stack’ine geri döner. A node’nun gidebileceği başka bir node kalmadığı için A node’nu da stackten sileriz. Böylelikle stackte hiçbir node kalmamış olur.
Aşama 18:
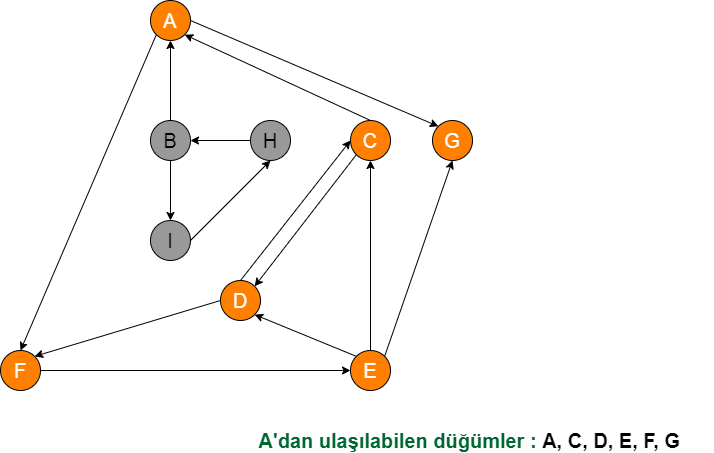
Derin Öncelikli Arama
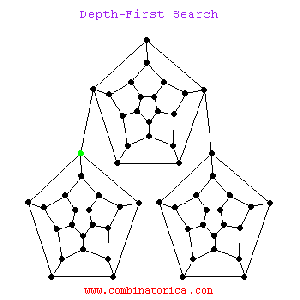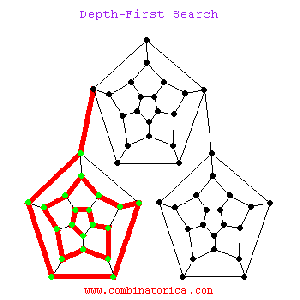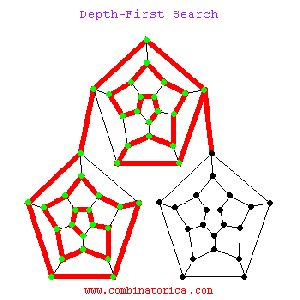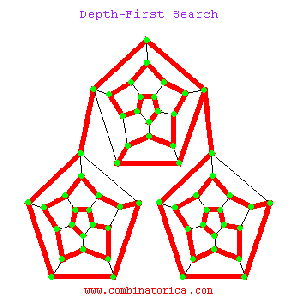
Kaynakça: Akifhatipoglu, Stanford, Dergipark, Geeksforgeeks, Tutorialspoint
ALGORITHMS COURSE – GRAPH THEORY TUTORIAL FROM A GOOGLE ENGINEER








Yorum Yap